1. Background
Before 221BC, China already knew the circle, and gave a definition, which is "The set of points in the plane whose distance from a fixed point is equal to a fixed length" (圆,一中同长也). In the 11th century BC, Shang Gao, a mathematician from the Western Zhou Dynasty in China, also discussed the relationship between circles and squares with the Duke of Zhou. After understanding the circle, people began to perform various calculations about the circle, especially calculating the area of the circle.
They used half of the circumference to multiply the radius and then got the area, which is C=πr^2(半周半径相乘得积步). They knew π, which is about 3, the ratio of circumference to diameter (周三径一). This way is very inaccurate. The circumference in fact is the circumference of a regular hexagon enclosing inside the circle.
Based on these experiences, ancient Chinese mathematicians conducted in-depth exploration and obtained the method of cutting circles to calculate π.
2. Cutting circle to calculate π.
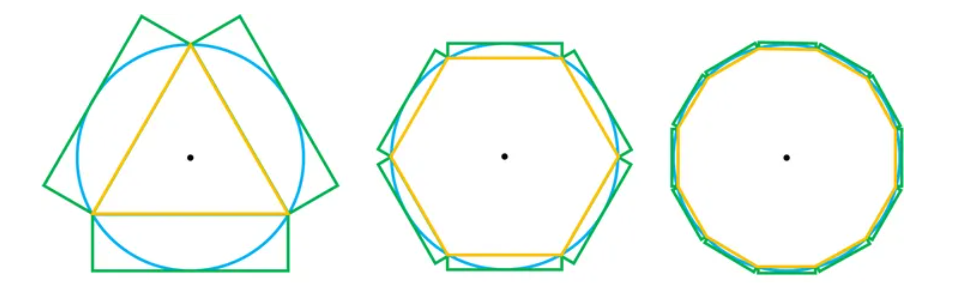
When Han Dynasty scientist Zhang Heng summarized the experience of his predecessors, he realized that the result of replacing the circumference of a circle with the circumference of an inscribed regular hexagon was very inaccurate. He suggested that it would be better to calculate demerits using circumscribed regular polygons. But after the Han Dynasty, Liu Hui, a mathematician in the Wei and Jin Dynasties, believed that the result would be larger than the circumference of the circle and was inaccurate. He used the idea of limits to cut the circle infinitely, and the perimeter of the polygon would become closer and closer to a circle (割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣。).
Following this idea, Liu Hui calculated the circumference of the regular polygon inscribed in the circle to the regular 3072 polygons, and thus obtained two approximate values of π, 3.1415 and 3.1416. This result was the most accurate data for pi calculation in the world at that time. Liu Hui was very confident in the new method of "circle cutting" he created, and extended it to all aspects of circular calculations, thereby greatly advancing the development of mathematics since the Han Dynasty. Later, during the Northern and Southern Dynasties, Zu Chongzhi continued to work on Liu Hui's work and finally made pi accurate to the seventh decimal place. In the West, this achievement was achieved by the French mathematician Veda in 1593, more than 1,100 years later than Zu Chongzhi. Zu Chongzhi also obtained two fractional values of pi, one is the "approximate ratio" and the other is the "density ratio". This value was only obtained in the West by Otto of Germany and Antonitz of the Netherlands at the end of the 16th century. , all eleven hundred years later than Zu Chongzhi. The new method of "circle cutting" created by Liu Hui made a significant contribution to the development of ancient Chinese mathematics. History will never forget it.
3. the calculation steps
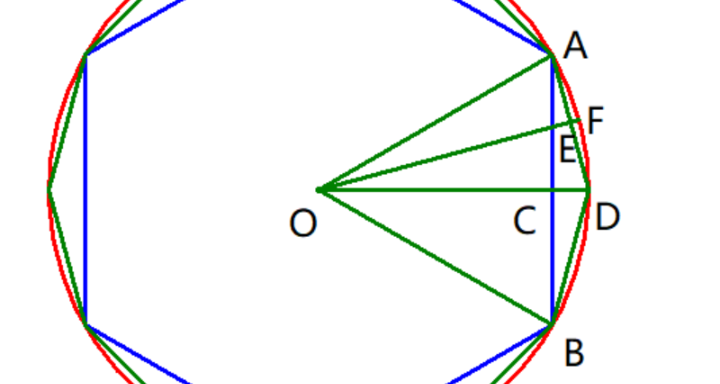
Assume that the radius of the circle is 1 and the side length of the regular hexagon inscribed in the circle is also 1. The side length of the regular 12-sided polygon can be calculated as follows:
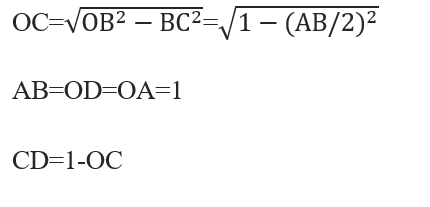
The new side of AD is
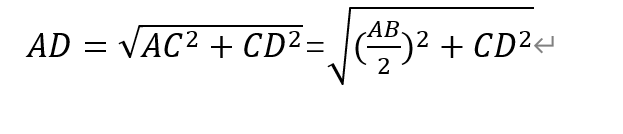
The length of AD is smaller, the circumference is more like the circumference of a circle, and π is the ratio of circumference and diameter.
4. How to achieve in Python
According to the above theory and formula. We can use python to accurately calculate the value of pi. As long as the number of sides of the regular polygon is enough, the calculated value of pi is accurate enough.
import math
def cutting_circle(times):
global pi
side_length = 1
edges = 6
def length(x):
h = math.sqrt(1 - (x / 2) ** 2)
return math.sqrt((x / 2) ** 2 + (1 - h) ** 2)
for i in range(times):
side_length = length(side_length)
edges *= 2
pi = side_length * edges / 2
return pi
if __name__ == '__main__':
times = input("write down the times you want: " )
times=int(times)
print('the times you cut is {},the pi is{:.6f}'.format(times, cutting_circle(times))) # pi
print('the pi in python math is{:.6f}'.format(math.pi))
This is the result. You can refer :